4.3. Правило лимитирующего звена для многовидовых сообществ, потребляющих взаимонезаменимые ресурсы
Возможный способ отбора лимитирующих факторов в общей экологии состоит в использовании законов сохранения потребляемых сообществом ресурсов с привлечением экстремальных принципов.
Для случая потребления многовидовым сообществом произвольного числа взаимонезаменимых ресурсов, количества которых заданы, и при отсутствии, кроме недостатка ресурсов, иных причин элиминации организмов из сообщества предлагается формулировка правила лимитирующего звена: совокупность потребностей видов сообщества в потребляемых ресурсах позволяет предсказать те ресурсы, которые могут быть потреблены сообществом из среды полностью и от которых только и зависят конечные биомассы видов.
Дополнительные предположения об экстремальных свойствах финальных состояний сообщества приводят к выводу о существовании в пространстве факторов среды областей, где рост популяций ограничен любой комбинацией из совокупности всех потребляемых сообществом взаимонезаменимых ресурсов.
В разделе 4.3 рассмотрены примеры выявления лимитирующего звена для сообщества луговых трав и для лабораторных альгоценозов (Левич и др., 1993б). Правило лимитирующего звена обобщает на многовидовые сообщества правило минимума Либиха и закон совокупного действия факторов Митчерлиха.
4.3.1. О принципах лимитирования в экологии
При обсуждении принципов лимитирования в экологии мы следуем работе Д. Г. Замолодчикова с соавт. (1993б).
Истоки концепции лимитирующих факторов восходят к немецкому агрохимику Юстусу Либиху, сформулировавшему в 1840 году знаменитый закон минимума (Leibig, 1840; имеется перевод: Либих, 1936): “Каждое поле содержит одно или несколько питательных веществ в минимуме и одно или несколько других в максимуме. Урожаи находятся в соответствии с этим минимумом питательных веществ...” (Либих, 1936, с.345). Следует особо отметить, что Ю.Либих понимал под минимумом относительный минимум питательного вещества по сравнению с содержанием остальных веществ: “... Закон минимума имеет силу не для одного только питательного вещества, но для всех. Если в данном случае урожаи какой-либо культуры ограничены вследствие минимума фосфорной кислоты в почве, то при увеличении количества фосфорной кислоты урожаи повысятся до такой величины, при которой прибавленная фосфорная кислота будет находиться в правильном соотношении с количеством другого питательного вещества, находящегося в минимуме” (Либих, 1936, с. 377). За фактором, который, по Либиху, находится в минимуме, позже в экологической литературе установилось название лимитирующего. Закон, аналогичный либиховскому, для процессов фотосинтеза в 1905 г. предложил Ф.Блэкман (Blackman, 1905), а в 1965 г. для скоростей ферментативных реакций — Н.Д.Иерусалимский (1965).
В 1909 году немецкий агрохимик Э.А.Митчерлих (Mitscherlich, 1909, 1925) сформулировал “закон физиологических взаимосвязей”, позднее переименованный в “закон совокупного действия факторов”. Митчерлих утверждал, что величина урожая зависит от уровней всех “факторов роста” и тем самым прямо противопоставлял свой закон принципу минимума Либиха. Последователь Митчерлиха Б.Бауле предложил эмпирическую формулу, выражающую величину урожая через уровни факторов роста при известной величине максимального урожая. Следует отметить,
что подавляющее большинство экспериментов, проведенных Митчерлихом и его последователями (Митчерлих, 1931; Кирсанов, 1931), относились к проверке предложенной формулы для одного фактора, однако в этом случае формула Митчерлиха-Бауле фактически представляет собой количественную интерпретацию принципа минимума.В 1913 году американский эколог В.Шелфорд (Shelford, 1913) выдвинул концепцию, известную в настоящее время как “закон толерантности”. Основой для концепции послужили зависимости количественных оценок тех или иных свойств популяций от важнейших факторов внешней среды (названные позже функциями отклика), имеющие колоколообразную форму. Сущность закона толерантности состоит в том, что как недостаток, так и избыток любого фактора может оказаться вредным для биологического объекта (организма, популяции). Пределы, в которых возможно существование организма, получили название диапазона толерантности. Под лимитирующим фактором в таком случае понимается тот, значение которого приближается или выходит за пределы толерантности.
В современной экологической литературе (Одум, 1975, 1986; Федоров, Гильманов, 1980; Пианка, 1981) закон толерантности рассматривается как прямое продолжение и расширение принципа минимума Либиха. Выше мы уже отмечали, что, по Либиху, лимитирующим является фактор, который содержится в относительном минимуме по сравнению с уровнями других факторов. При этом его уровень может находиться в любой точке диапазона толерантности по данному фактору. Таким образом, принцип Либиха относится к выбору лимитирующего (т. е. определяющего продуктивность, обилие или другие экологические характеристики популяции) фактора из всей совокупности факторов при условии, что уровни их находятся в пределах толерантности.
Исходя из концепции Шелфорда, В.Д.Федоров и Т.Г.Гильманов (1980) определяют лимитирующий фактор как тот, по которому для достижения заданного относительного изменения функции отклика требуется минимальное относительное изменение значения фактора. Под функцией отклика в данном случае понимается частная функция отклика, складывающаяся при данных значениях экологических факторов. Подобный подход требует подробного изучения зависимости функции отклика от всей совокупности экологических факторов в каждом конкретном случае, что связано с использованием приемов многофакторного эксперимента и аппарата многомерной математической статистики. Очевидно, что при всей теоретической привлекательности такого способа его практическое использование может оказаться ограниченным из-за недостатка нужных эмпирических данных.
Современные практические подходы к выделению лимитирующих факторов фактически сводятся к двум классическим концепциям — принципу минимума Либиха и закону совокупного действия факторов Митчерлиха. Принцип минимума Либиха трансформировался на практике в концепцию сбалансированных соотношений питательных элементов в среде, активно применяющуюся в областях, связанных с культивированием растительных организмов — агрохимии и альгологии (
Ahlgren, 1980; Ринькис, Ноллендорф, 1982; Groot, 1983; Церлинг, 1990; заметим, что применение принципов лимитирования в гидробиологии обосновал С.А.Зернов, 1934).Другой областью экологии, где часто возникает проблема лимитирующих факторов, является математическое моделирование экосистем. Фактически все модели, использующие описание скоростей роста популяций или сообществ растительных организмов, основываются либо на принципе Либиха, либо на законе Митчерлиха (Страшкраба, Гнаук, 1989). В первом случае общая скорость моделируемого процесса определяется минимальной из скоростей потребления биогенных элементов (Полетаев, 1973; Умнов, 1973;
Larsen et al., 1974; Bierman, 1976; Алексеев, Сазыкина, 1981), во втором — функциональной комбинацией скоростей потребления всех питательных элементов (Patten et al., 1975; Семевский, Семенов, 1982). Для систем первого типа И.А.Полетаев (1973) предложил название “системы Либиха”, второй путь фактически является какой-либо математической экспликацией закона Митчерлиха. Проиллюстрируем простейшие (и наиболее употребимые) из способов использования закона Либиха в системах дифференциальных уравнений для относительной скорости роста m:![]()
и закона Митчерлиха:
![]()
в случае потенциального ограничения роста тремя факторами — интенсивностью света (I), содержанием фосфора (P) и азота (N); здесь K с соответствующими индексами — константы полунасыщения.
Следует отметить, что исходные формулировки принципов лимитирования как Либих, так и Митчерлих относят к популяциям одного вида. В то же время на практике эти принципы часто используются в применении к многовидовым сообществам. Например, в моделях водных экосистем, упоминавшихся выше, описываются скорости роста агрегированного фитопланктонного сообщества, в действительности состоящего из значительного количества видов. Таким образом, концепция лимитирующих факторов в применении к сообществам организмов требует определенной теоретической проработки, которая и предлагается в настоящем разделе книги.
В первую очередь, необходимо ответить на следующие вопросы:
4.3.2. Предлимитирующие факторы
Факториальная экология выделяет факторы среды, которые можно было бы назвать физиологическими (например, температуру, водородный показатель) и ресурсными (энергетические и субстратные компоненты питания). Законы толерантности относятся в первую очередь к физиологическим факторам, а законы лимитирования — исключительно к ресурсным. Контекст настоящего исследования относится к анализу условий роста многовидовых сообществ при потреблении нескольких взаимонезаменимых ресурсных факторов и при благоприятных (толерантных) значениях физиологических факторов. Ресурсные факторы назовем лимитирующими, если при остановке роста биосистемы (например, популяции, сообщества) добавление этих факторов в среду (например, в почву, воду) приводит к возобновлению роста.
Задачу о поиске лимитирующих факторов будем решать на основании законов сохранения потребляемых сообществом ресурсов:
![]() . (19)
. (19)
Здесь n
i — численность вида i в момент остановки роста полной численности сообщества. ПотребностиЕсли выполнены два условия — во-первых, толерантны все физиологические факторы и, во-вторых, учтены все ресурсные факторы в системе (19), — то можно быть уверенными в том, что остановка роста сообщества вызвана исчерпанием в среде какой-либо части (хотя бы одного) потребляемых сообществом ресурсов (если пренебречь остающимися в среде пороговыми концентрациями ресурсных факторов). Другими словами, некоторые из нестрогих неравенств системы (19) в момент остановки роста обязательно становятся равенствами. Предположим, что в момент остановки роста мы добавим для потребления в среду дополнительные количества ресурсов. Очевидно, что добавление тех веществ, которые не были потреблены полностью (в системе (19) для них выполняются строгие неравенства), не вызовет возобновление роста, т.е. они не могут быть лимитирующими. Добавление тех же веществ, что уже были полностью использованы, ликвидирует причину остановки роста. Напомним, что в рассматриваемом контексте нас интересуют только те причины остановки, что связаны с ресурсными факторами. В приведенном рассуждении неявно подразумевается, что в живой природе действует принцип расширенного самовоспроизводства организмов при отсутствии ограничивающих рост факторов. Этот принцип не позволяет надорганизменным системам останавливать рост популяций при наличии неисчерпанных ресурсов. Для лимитирующих факторов появляется эквивалентное приведенному выше определение: это ресурсы, которые потребляются сообществом из среды полностью (с точностью до пороговых концентраций), или на формальном языке — ресурсы, для которых в системе (19) выполняется строгое равенство. Первый этап задачи поиска лимитирующих факторов приобретает формальную постановку: при заданных потребностях видов сообщества
Вместо использованных в системе (19) введем более лаконичные обозначения:
n
º {n1, n2, ..., nw}, D º {D1, D2, ..., Dm} и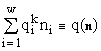 .
.
Определим в m-мерном пространстве факторов D
1´ D2´ ...´ Dm два многомерных тела: конус K(q) и параллелепипед P(D). Выпуклый конус K(q) есть неотрицательная линейная оболочка совокупности w векторов qi (q(
n) £ D,есть пересечение тел конуса K(q) и параллелепипеда P(
D) (заштрихованная область на рис. 4.11). Таким образом, если вектор D лежит внутри конуса K(q), определяемого матрицей потребностей сообществаПриведенные рассуждения (вместе с доказательствами из цитированной работы) позволяют сформулировать теорему предлимитирующего звена: система (19) q(
n)£ D равносильна системе: ![]() , (20)
, (20)
которая получается из (19) вычеркиванием строк с теми компонентами
D, что не могут быть потреблены полностью. При этом для системы (19) существует хотя бы один фактор, который может быть потреблен полностью (поскольку неограниченный конус обязан пересекаться с ограниченным параллелепипедом хотя бы по одной грани).Удобно назвать факторы из вектора

равносильна системе
4.3.3. Учет экстремальных принципов
Система (19), как и редуцированная согласно правилу лимитирующего звена система (20), имеет, как правило, множество решений, состоящее из большого числа элементов. Одним из принятых в естествознании способов выбора ограниченного набора реальных состояний из совокупности всех потенциально возможных является выбор состояний, удовлетворяющих требованию экстремальности некоторого функционала (подробнее см. Левич, 1988).
Одним из вариантов экстремального принципа может быть принцип полного потребления (Левич, Лебедь, 1987): все факторы, которые могут быть потреблены полностью, именно так и потребляются сообществом, т. е. речь идет о максимальном потреблении сообществом доступных ресурсов. Другими словами, все предлимитирующие факторы в случае принятия принципа полного потребления по определению считаются лимитирующими. И поиск лимитирующих факторов сводится к однозначным процедурам теоремы о предлимитирующем звене. Эвристически принцип полного потребления согласуется с принципом максимальной экспансии живого, которой, естественно, сопутствует максимальное вовлечение в жизненный оборот абиотических ресурсов. Примеры поиска лимитирующих факторов для ситуаций с полным потреблением рассмотрены в следующем разделе настоящей работы. Заметим, что принцип полного потребления на формальном языке означает переход от системы q(
n) £ D к системеВ
экологии сообществ находит применение и энтропийный экстремальный принцип (см. 4.1), позволяющий выделить единственное реальное состояние из всех, допустимых законами сохранения (19). При этом оказывается (Левич и др., 1994), что внутри любого конуса K(q) существует конусДоказана (Левич и др., 1994) теорема стратификации: все пространство
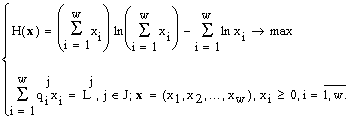 (21)
(21)
Биологическую интерпретацию факторов j Î J, порождающих страты S
J, предлагается соотносить с экологической концепцией лимитирующих факторов. Было предложено (см. 4.3.1) следующее определение: ресурсный фактор будет называться лимитирующим, если при остановке роста биосистемы добавление этого фактора в среду приводит к возобновлению роста. Там же было показано, что фактор j Î {1; 2; ...; m} является лимитирующим тогда и только тогда, когда на решении x вариационной задачи (4) мы имеем равенствоа) потребляются полностью (т.е. являются лимитирующими в смысле, указанном выше);
б) являются аргументами экстремали (7) (т.е. оказываются лимитирующими в том смысле, что x
i, i =Перечислим несколько следствий из теоремы стратификации.
4.3.4. Примеры выявления лимитирующих факторов
Применение принципа лимитирующего звена (Замолодчиков и др., 1993) требует количественных оценок потребностей биологических видов в ресурсах среды. Представления о потребностях видов в субстратных факторах были введены Ю.Либихом (Leibig, 1840) при определении сбалансированного соотношения питательных веществ в почве при возделывании различных сельскохозяйственных культур. В качестве количественной оценки потребностей Ю.Либих использовал содержание питательных веществ в биомассе растений. За время, прошедшее после работ Ю.Либиха, данный подход получил широкое распространение. В агрономии определение оптимальных количеств удобрений строится на величинах выноса веществ с урожаем, т. е. с помощью знаний о потребностях сельскохозяйственных культур. В литературе накоплено значительное количество сведений по содержанию биогенных элементов в культурных растениях.
Первый пример, иллюстрирующий применение правила лимитирующего звена, касается трехвидового сообщества, состоящего из тимофеевки, костреца безостого и ежи сборной. Данный агроценоз может использоваться для получения кормовой массы. Рассмотрим процедуру определения характера лимитирования при потенциальном ограничении роста сообщества двумя субстратными факторами (азотом и фосфором).
Согласно правилу лимитирующего звена (при использовании принципа полного потребления), двухфакторное лимитирование будет иметь место в том случае, когда
![]() ,
,
где
Если использовать энтропийный экстремальный принцип, то характер лимитирования при потенциальном ограничении роста сообщества двумя субстратными факторами D
1 и D2 рассчитывается по параметрам n0 и n1 из формулы (13), которые определяют границыv0 £ D1/D2 £ v1,
лимитируют оба фактора, когда D
1/D2 < n0, лимитирует первый фактор, а когда D1/D2 > n1 — второй. Указанные неравенства задают конусРасчет лимитирующего звена с использованием энтропийного экстремального принципа показывает (табл. 4.8), что область значений факторов, в которой наблюдается двухфактор
-¤
ное лимитирование, существенно уже, чем при использовании принципа полного потребления. Ситуация двухфакторного лимитирования в приведенном примере реализуется лишь для почвы с содержанием в 100 граммах 4 мг фосфора и 40 мг азота.
Представления о потребностях видов в субстратных факторах разработаны также в альгологии (см. гл. 1), поэтому для дальнейшей иллюстрации мы обратимся к результатам исследований лабораторных альгоценозов.
Для планктонных микроводорослей под потребностью в субстратном факторе принимают минимальную клеточную квоту, то есть содержание субстратного фактора в клетке к моменту остановки роста клетки из-за недостатка данного фактора. Эксперименты с монокультурами микроводорослей позволяют вычислить величины минимальных клеточных квот (гл. 1), которые затем можно использовать для определения характера лимитирования в поликультурах. В настоящей работе мы пользуемся величинами потребностей видов микроводорослей в субстратных факторах, приведенными в работе А.П.Левича и В.И.Артюховой (1991, см. также гл. 1).
Рассмотрим характер лимитирования при потенциальном ограничении роста сообществом из четырех видов микроводорослей (
Scenedesmus quadricauda, Scenedesmus obliquus, Ankistrodesmus falcatus, Chlorella vulgaris) двумя субстратными факторами (азотом и фосфором). Критерии для определения характера лимитирования при использовании как принципа полного потребления, так и энтропийного принципа, аналогичны приведенным выше для травяного сообщества. Расчеты с использованием принципа полного потребления показывают (табл. 4.9), что для сообщества из четырех видов водорослей на среде с 0.05 мг/л фосфора и 6 мг/л азота лимитирующим фактором будет фосфор, а на средах, в которых содержание фосфора повышено до 0.1 и 0.2 мг/л, лимитирующее звено состоит из обоих факторов — азота и фосфора. При использовании энтропийного экстремального принципа двухфакторное лимитирование имеет место лишь на среде с 0.20 мг/л фосфора и 6 мг/л азота.В том случае, когда рост сообщества потенциально ограничен тремя и более факторами, выяснение характера лимитирования сводится (при использовании принципа полного потребления) к простым алгоритмам линейного программирования.
Рассмотрим пример определения характера лимитирования при потенциальном ограничении роста лабораторного альгоценоза тремя факторами. Помимо основных биогенных элементов, важным для жизнедеятельности микроводорослей фактором является свет. Видоспецифическую потребность в свете водорослевой клетки (q
E) можно охарактеризовать величиной, пропорциональной квадратному корню от объема клетки (гл. 1).Измеренные величины потребностей видов водорослей и характеристики световых условий приведены в табл. 4.10. Вычисления с использованием принципа полного потребления показывают, что на среде с 6 мг/л азота и 0.05 мг/л фосфора лимитирующее звено состоит из одного фактора — фосфора; на среде с 6 мг/л азота и 0.1 мг/л фосфора звено состоит из света и фосфора; на средах, в которых количество фосфора повышено до 0.2 и 0.3 мг/л, в лимитирующее звено входят все три фактора — азот, фосфор и свет.
В случае трех и более факторов формулы, задающие конус
Приведенные примеры показывают, насколько важен при определении характера лимитирования полный охват потенциально лимитирующих факторов. Действительно, содержание биогенных элементов при рассмотрении потенциального ограничения роста двумя (табл. 4.9) и тремя факторами (табл. 4.10) на соответствующих средах одинаково, однако введение третьего фактора существенно изменяет вид лимитирующего звена для ряда сред. Разобранные примеры свидетельствуют также, что состав лимитирующего звена существенно зависит от исповедуемого экстремального принципа.
4.3.5. Следствия из правила лимитирующего звена
Рассмотренные примеры относились к небольшому числу действующих факторов (m
= 1, 2 или 3). Подчеркнем еще раз, что однозначные процедуры расчета лимитирующего звена существуют для произвольного числа факторов среды m и любого числа видов w.Первое следствие из правила лимитирующего звена касается одновидовых сообществ. Заметим, что в этом случае конус K(q) (а следовательно, и
![]()
Пусть w
= 1, тогдаD1/D2 < q1/q2
, или D1/q1 < D2/q2. (22)Таким образом, лимитирующим оказывается фактор, находящийся в минимуме в смысле неравенства (22). Напомним, что лимитирующим был назван фактор, добавление которого после остановки роста сообщества приводит к возобновлению роста. Было показано, что лимитирующий ресурс потребляется популяциями из среды полностью. Рост одновидовых сообществ лимитируется фактором, обеспечивающим наименьший возможный прирост численности D
k/qk при заданном запасе ресурса Dk и потребности qk в нем особей популяции. Приведенное утверждение, вводя меру qk потребности особей в заданном факторе k, дает строгую экспликацию представлений о “минимуме” факторов, и принцип минимума Либиха становится частным случаем (для w = 1) теоремы о лимитирующем звене.Второе следствие относится к противоречию между принципом Либиха, указывающим на единственность лимитирующего фактора, и принципом Митчерлиха, отстаивающим существенность для роста одновременно всех потребляемых ресурсов. Заметим, что исходная либиховская формулировка принципа минимума подразумевает возможность ограничения роста сразу несколькими факторами. Такая ситуация имеет место, когда величины D
k/qk равны и минимальны для нескольких факторов. Если же данные величины равны для всех потребляемых факторов, то лимитирующими (т. е. полностью потребляемыми) являются все факторы, а среду можно считать сбалансированной. В этом случае справедливым оказывается закон совокупного действия факторов Митчерлиха. Заметим, что законы Либиха и Митчерлиха применимы только для одновидовых сообществ, т.е. для отдельных популяций. На рис. 4.12 (w=1, m=2) приведен пример сбалансированной среды D для одновидового сообщества. Правило лимитирующего звена обобщает указанную ситуацию на многовидовые сообщества и снимает оппозицию между принципами Либиха и Митчерлиха: в пространстве факторов среды существуют области, где рост сообщества ограничен любой комбинацией из совокупности всех потребляемых сообществом факторов, в частности — любым единственным фактором, любыми несколькими или сразу всеми факторами. Это утверждение составляет содержание строгой теоремы, верной для любых распределений потребностейБиологический смысл вычислительных процедур по отысканию лимитирующего звена прозрачен: обобщается идея, точно реализующаяся в случае одновидовых сообществ, а именно, ищутся факторы, которые способны обеспечить в определенном смысле наименьший прирост численности видов при заданных запасах ресурсов D
k и заданных потребностяхТаким образом, можно сделать вывод, что правило лимитирующего звена обобщает и эксплицирует законы лимитирования Либиха и Митчерлиха на сообщества, содержащие произвольное число видов и потребляющие произвольное число факторов. Закон толерантности Шелфорда дополняет правило лимитирующего звена для физиологических факторов и в области повышенных уровней ресурсных факторов.
Правило лимитирующего звена основывается на законах сохранения вещества и энергии, на представлении о минимальных потребностях организмов в субстратно-энергетических факторах, на экстремальных экологических принципах. Некоторые из этих обоснований требуют экспериментальной проверки. Варианты опыта, в которых вектор потребляемых ресурсов
D находился бы вне конуса потребления K(q), между конусами K(q) иПравило лимитирующего звена было предложено нами на основании модели, рассматривающей сообщество, лимитируемое только взаимонезаменимыми ресурсами, для которых в системе “сообщество-ресурсы” выполняются законы сохранения. Очевидно, что данная модель, и, следовательно, полученные выводы не являются справедливыми для всех экологических сообществ. В частности, при лимитировании сообщества не ресурсными факторами, а например, следующим трофическим уровнем, так же при лимитировании взаимозаменимыми ресурсами и т. д. Тем не менее класс сообществ, лимитирование в которых близко к рассмотренному в данной главе, достаточно широк и включает в себя большинство растительных сообществ, лимитируемых биогенными элементами, микроэлементами и светом. Следует отметить, что под действие принципа лимитирующего звена попадает также большинство из растительных сообществ, используемых в сельском хозяйстве, и многие из микробиологических сообществ, эксплуатируемых в биотехнологической промышленности.
4.4. Теорема оптимизации структуры экологических сообществ
Выбор модели. Поиск путей и стратегий управления экологическими объектами вряд ли возможен чисто эмпирическим путем. Поэтому решение проблемы биоманипуляций требует предварительного модельного анализа. Предлагается решать задачу оптимизации (Левич и др., 1993а) в рамках процедуры, основанной на моделировании экологического сообщества с помощью структуры множеств с разбиением (см. 4.1).
Напомним, что решение вариационной задачи методом Лагранжа дает экстремаль:
![]() ,
,
называемую формулой видовой структуры. Множители Лагранжа d
k ищутся из системы алгебраических уравнений:  (23)
(23)
Случай двухфакторного лимитирования
. Случай m=1 не рассматривается, так как из первого уравнения системы (23) мы находим, что d1 не зависит от L1. Следовательно, относительная численность i-го видаРассмотрим отдельно случай
m=2 как наиболее часто встречающийся в эксперименте и вместе с тем допускающий наглядное аналитическое исследование.Если ввести обозначения ex
p(-d1) =x, exp(-d2) =y, то система (23) запишется в виде: 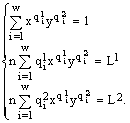 (24)
(24)
Так как нас интересуют относительные численности
ji(t) = ni/n =  (25)
(25)
где t=L
1/L2.Анализ системы (25) (Левич и др., 1993а) дает полную картину поведения относительных численностей видов сообщества при
При
![]() (26)
(26)
не имеет решений n
i ³ 0 (![]() .
.
При
Чтобы проиллюстрировать поведение относительных численностей видов при модификациях среды, с помощью ЭВМ были построены графики
ji(t), полученные путем решения системы (25) приСлучай произвольного пространства факторов. Рассмотрим теперь случай m ³ 3. И в этом случае экстремальная модель дает выделенные для данного вида отношения веществ среды, равные отношениям его потребностей.
Обозначим exp(-d
k) =xk,
 (27)
(27)
Относительная численность вида i дается формулой
ji =Решая эту задачу методом множителей Лагранжа, получим необходимое условие для того, чтобы точка (x
1, x2, ..., xm) давала экстремум в виде системы:  (28)
(28)
Сравнивая (27) и (28), видим, что они совпадают при L
k/L1 =Еще раз сформулируем полученные результаты: относительные численности видов зависят только от отношений полностью потребляемых сообществом ресурсов среды;
заданному набору ресурсов среды
L соответствует единственное состояние сообщества n;относительная численность заданного вида принимает наибольшее значение при отношениях в среде ресурсных факторов, равных отношениям потребностей в них данного вида.
(Отметим, что к аналогичному выводу приводит и исследование имитационной модели, см. гл. 5.)4.5. Подбор видов планктонных водорослей для полной утилизации многобиогенной нагрузки на водоем
Совокупность потребностей некоторого вида в субстратно-энергетических факторах среды можно назвать ресурсной структурой популяции (Левич, 1980; Левич, Лебедь, 1987). Рассмотрим сообщество, состоящее из w видов, которые потребляют из среды m общих субстратов (Замолодчиков, Левич, 1992). Возникает вопрос, в какой мере ресурсная структура сообщества определяет его видовую структуру — численности входящих в сообщество видов, а также количества потребляемых сообществом веществ. Соотношение между ресурсной и видовой структурой сообщества, с одной стороны, и факторами среды — с другой, задаются балансовыми равенствами законов сохранения веществ и энергии:
![]() . (29)
. (29)
Здесь n
i — численность вида i к моменту потребления всем сообществом факторовКоличество популяций w в сообществах видов, существующих на общих субстратах, как правило, превышает количество существенных факторов среды m. Реальность такой ситуации вступает в противоречие с принципом конкурентного исключения, согласно которому на m субстратах могут существовать не более чем m различных видов.
Указанное противоречие привело, например, в гидробиологии к констатированию парадокса одновременного существования десятков симпатрических видов (Hutchinson, 1959) и позднее — к формулировке принципов сосуществования (Ghilarov, 1984) или конгруэнтного перекрывания (Mikhailovsky, 1986) как альтернативы конкурентному исключению. Таким образом, система (29) из m равенств для w неизвестных величин n
i не может дать ответ на основной вопрос экологии сообществ: какова численность каждого из видов сообщества при заданных количествах потребленных из среды факторов.Тем не менее анализ системы (29) помогает дать ответы на целый ряд вопросов экологии сообществ. Один из таких вопросов может быть сформулирован как задача подбора видов для утилизации многобиогенной нагрузки на водоем. Иными словами, каков должен быть видовой состав сообщества для полной утилизации данного количества субстратных факторов. Решение проблем такого рода может иметь важное практическое значение, например при биологической очистке воды; в биотехнологических системах, основанных на планктонных водорослях, и т. д.
Проведем анализ системы (29). На математическом языке речь идет о линейном отображении q: R
w® Rm из неотрицательного квадранта w-мерного пространства численностей видов в положительный квадрант m-мерного пространства количеств факторов среды. Отображение q задается матрицей потребностейОбласть существования решения системы (29) в пространстве R
m факторов среды есть выпуклый конус K(q), являющийся неотрицательной линейной оболочкой совокупности w векторов потребностей qi (Положение вектора
D внутри области K означает, что соответствующие этому вектору соотношения компонентов среды являются сбалансированными: существуют сообщества, потребляющие эти компоненты полностью. На рис. 4.14 точка А лежит внутри конуса К, и потому соответствующие ей содержания факторов D1 и D2 могут быть полностью потреблены имеющимся сообществом. Если же вектор D лежит вне области существования сообщества, то имеющиеся количества факторов не могут быть потреблены сообществом полностью, причем анализ системы (29) позволяет для любых размерностей пространства факторов m и пространства видов w указать границы потребления каждого из факторов. Например, на рис. 4.14 точка B лежит вне конуса K, при этом фактор D2 может потребляться сообществом полностью, а фактор D1 — только до пределов значения D1B. После потребления имеющихся количеств фактора D2 развитие сообщества останавливается за его отсутствием, и поэтому данный фактор можно назвать лимитирующим.Роль различных видов сообщества неодинакова по отношению к области его существования. Вектора потребностей одних видов — назовем их определяющими — порождают ребра конуса K, для других видов эти векторы лежат внутри конуса или на его гранях. Элиминация из сообщества определяющих видов приводит к сужению области K, а отсутствие остальных видов не меняет K. На рис. 4.14 определяющими являются виды 1 и 5. Если же рассматривать конкретное значение вектора
D (например, в точке A), то окажется, что достаточно иметь в качестве определяющих виды 3 и 4, чтобы количества факторов D1 и D2 потребились полностью. Можно обобщить, что исходные количества факторов будут полностью потреблены в том случае, если в сообществе среди определяющих есть виды, лимитированные по каждому из имеющихся факторов. Например, для точки А на рис. 4.14 фактором D1 лимитируются виды 4 и 5, а фактором D2 — виды 1, 2 и 3. Тогда количества факторов, соответствующие точке А, будут потреблены сообществом, в котором одновременно присутствуют хотя бы по одному виду из группы видов 3-4 и группы 1-2-3.Таким образом, если известны клеточные квоты для каких-либо видов фитопланктона, то можно произвести подбор видов для сред с конкретными значениями факторов. Для примера нами были использованы значения клеточных квот по азоту и фосфору для семи видов планктонных водорослей (табл. 1.1). Предположим, следует определить, каким сообществом может быть полностью потреблена среда с 25 мг/л азота и 1 мг/л фосфора. Следует отметить, что здесь и далее мы будем использовать в рассуждениях значения факторов в среде, которые отличаются от значений вектора
D на начальные содержания факторов в видах. Однако в практических задачах (например, при альголизации сточных вод) содержание факторов в среде существенно превосходит содержание их во вносимых водорослях, и поэтому можно считать, что вектор D близок к вектору содержания факторов в среде L.Для начала определим, какие из видов табл. 1.1 лимитируются азотом, а какие — фосфором (при содержании в среде азота 25 мг/л и фосфора 1 мг/л). Если отношение N:P в клеточных квотах превосходит отношение N:P в среде, то лимитирующим фактором для данного вида будет азот, и, соответственно, если меньше — то фосфор. Так как соотношение N:P в среде составляет 25, то по фосфору будут лимитированы
Scenedesmus obliquus, Ankistrodesmus falcatus, Anacystis nidulans, Anabaena variabilis, а по азоту — Chlorella ellipsoidea, Chlorella sp., Scenedesmus quadricauda (табл. 1.1). Тогда полностью количества азота и фосфора в среде будут потреблены сообществом, в составе которого есть хотя бы по одному виду из группы P-лимитированных и N-лимитированных. Например, такое сообщество может состоять из Chlorella sp. и Anacystis nidulans, или из Scenedesmus quadricauda и Scenedesmus obliquus. В сообществе может быть и более одного вида из каждой группы, но присутствие хотя бы одного из разных групп необходимо. Вектора потребностей указанных 7 видов и положение вектора значения факторов в среде (точка А) показаны на рис. 4.15. На нем отмечен также способ достижения полной утилизации факторов в точке А с помощью сообщества из двух видов: Chlorella ellipsoidea и Scenedesmus obliquus.Рассмотрим более сложный случай, когда размерность пространства факторов равна 3. В нашем распоряжении отсутствовали экспериментальные значения клеточных квот одновременно для трех факторов, поэтому в примере мы использовали гипотетические значения клеточных квот по трем факторам — кремнию, азоту, фосфору для 7 условных видов водорослей (табл. 4.11). Предположим, что следует составить сообщество, полностью потребляющее среду с соотношением Si:N:P, равным 25:12:1. Определим, каким из факторов в этом случае будут лимитироваться виды из табл. 4.11. Найдем парные отношения клеточных квот (Si:N, Si:P, N:P) и сравним их с парными отношениями содержания факторов в среде. Если отношение клеточных квот превышает отношение факторов в среде, то лимитирующим в данной паре будет фактор из числителя дроби, а если не превышает — из знаменателя. Фактор, лимитирующий по отношению к двум другим факторам, можно назвать общим лимитирующим фактором вида для данной среды. В нашем примере (табл. 4.11) у видов
1, 4, 7 общим лимитирующим фактором будет азот, видов 2 и 5 — фосфор, видов 3 и 6 — кремний. Факторы в среде будут полностью потреблены сообществом, в котором есть хотя бы по одному виду из каждой группы, например 4, 5, 6.Аналогичным будет и процесс выбора видов для четырех факторов. Рассматривать в этом случае следует шесть парных соотношений клеточных квот и содержания факторов в среде; общим лимитирующим фактором будет фактор, лимитирующий по отношению к трем другим, среда будет полностью потреблена сообществом, в котором есть хотя бы по одному виду из каждой группы, выделенных по четырем общим лимитирующим факторам. В принципе данный алгоритм применим к любой размерности пространства факторов, хотя объем вычислительной работы существенно увеличивается при возрастании числа факторов.
Следует отметить, что задачу подбора видов можно поставить несколько по-иному. В наших примерах мы выбирали виды по имеющемуся списку. Однако вопрос можно поставить так: каким соотношением квот должны обладать виды сообщества, чтобы потребить данную среду? Возвратимся к примеру для двух факторов — азота и фосфора. Для потребления среды с соотношением N:P, равным 25, необходимо иметь два вида, у одного из которых соотношение N:P клеточных квот меньше 25, а у другого — больше. Для трех факторов следует сформулировать требования к трем группам видов по парным соотношениям клеточных квот. Для среды с соотношением Si:N:P, равным 25:12:1, у Si-лимитированной группы видов отношение Si:N должно быть больше 2.1, а Si:P — больше 25. У
N-лимитированной группы Si:N должно быть меньше 2.1, а N:P — больше 12. У P-лимитированной группы Si:P меньше 25, а N:P — меньше 12. Разбив виды на группы согласно данным условиям, можно составить сообщество, включающее хотя бы по одному виду из каждой группы, которое полностью потребит имеющиеся количества факторов.В заключение следует отметить, что в некоторых случаях количество видов, необходимых для потребления m факторов, может быть и меньше m. Такое явление имеет место, когда соотношение клеточных квот равно соотношению содержаний факторов в среде. Например, вид с соотношением N:P клеточных квот 25 полностью потребит среду с 25 мг/л азота и 1 мг/л фосфора. Этот случай иллюстрирует точка С на рис. 4.14. В общем случае совпадение по одной паре отношений квот и содержания факторов уменьшает на единицу количество видов, необходимых для полного потребления факторов.